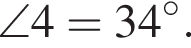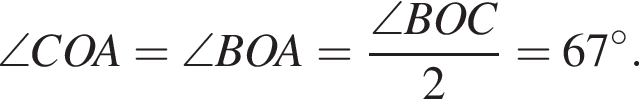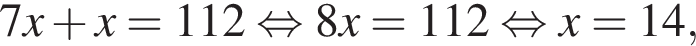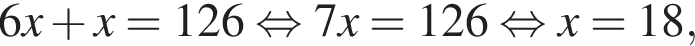На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что 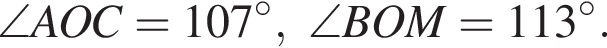 Найдите величину угла BOC.
Найдите величину угла BOC.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
На рисунке две прямые пересекаются в точке О. Если
 то угол BOC равен:
то угол BOC равен:
На рисунке a || b, 
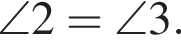 Найдите градусную меру угла 4.
Найдите градусную меру угла 4.
Из точки A к окружности с центром O проведены две касательные AB и AC, где B и C — точки касания. Через точки C и O проведена прямая, которая пересекает касательную AB в точке M (см. рис.). Найдите градусную меру угла 1, если ∠AMC = 44°.
Используя данные рисунка, найдите градусную меру угла 1 треугольника АВС.
Градусная мера угла ABC равна 112°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 7 (cм. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.

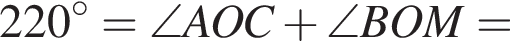

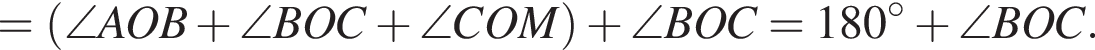



 равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°. равна 360°, поэтому
равна 360°, поэтому  равен 60°. Углы
равен 60°. Углы 
 Значит,
Значит, 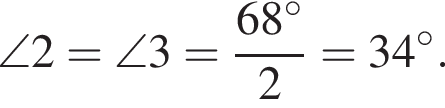 Тогда и
Тогда и